目前,重型商用車普遍安裝氣壓鼓式制動器,與其他結構的制動器相比,它具有制動力矩大、結構相對簡單以及價格便宜等優(yōu)勢,但是頻繁制動后鼓式制動器的溫升會導致制動效能急劇下降,出現(xiàn)制動熱衰退現(xiàn)象的缺點也十分明顯,這種現(xiàn)象在車輛超載、超速行駛時更為顯著。調查發(fā)現(xiàn),重型商用車出現(xiàn)制動失效的故障絕大部分是由熱衰退引起的。因此,探究車輛載荷、行駛速度和制動距離對制動熱衰退的影響尤為重要。
國內對鼓式制動器熱衰退的研究主要是通過選定某一試驗車型在某典型高速公路的長下坡路段進行實地測試,記錄制動鼓表面的溫度,分析制動鼓溫度與坡長、坡度、車速和車重的關系。這類研究的不足之處在于測試過程情況復雜,一致性難以保證;另外,實車測試只能記錄制動鼓外表面的溫度,缺乏對熱衰退過程中制動力矩的監(jiān)測。此次研究結合汽車行業(yè)標準QC/T 239-2015《商用車輛行車制動器技術要求及臺架試驗方法》,應用重型商用車制動器慣性試驗臺架,模擬東風某重型商用車的氣壓鼓式制動器在長下坡持續(xù)制動工況下,分析車速、載荷和制動距離對制動器溫升的影響。
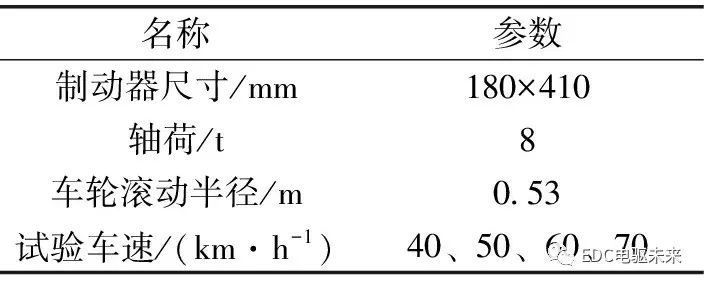
根據對312國道馬家坡和藍小路兩個長下坡路段所經過車輛的統(tǒng)計分析中發(fā)現(xiàn),貨車生產廠家中東風商用車占比高達71%,貨車軸型中三軸載貨車比例為42%。因此,此次選用東風商用車公司生產的某三軸車型的鼓式制動器作為研究對象具有一定的普遍性。結合蘇波等人根據跟車及問卷調查,發(fā)現(xiàn)大貨車在長下坡路段車速為40~65 km/h,并且下坡過程中基本能保持勻速狀態(tài)。因此,試驗車速擬設定為40、50、60和70 km/h。臺架試驗所需參數(shù)如表1所示。
表1 試驗參數(shù)
1.1 試驗準備
1.1.1 試驗臺主軸轉速的計算
制動器慣性試驗臺主軸轉速與車速按如下關系換算:
n=2.65v/r
式中:n為制動器慣性試驗臺主軸轉速,r/min;v為試驗車速,km/h;r為車輪滾動半徑,m。
根據上述公式,計算得到試驗車速對應的轉速如表2所示。
表2 試驗轉速

1.1.2 試驗轉動慣量的計算
試驗轉動慣量按下式進行計算:
I=mr2
式中:I為轉動慣量計算值,kg·m2;m為將汽車最大設計總質量按制動力分配比設計值分配給被試制動器所對應車輪承受的那部分質量,kg;r為車輪滾動半徑,m。
經過上述公式計算得到制動器滿載和超載時的試驗轉動慣量,如表3所示。
表3 試驗轉動慣量

1.2 熱電偶的安裝方式
引起熱衰退現(xiàn)象的主要因素是制動器溫度的上升使制動力矩急劇衰減,因此摸清熱衰退過程中制動蹄片和制動鼓的溫度變化尤為重要。參照QC/T 556-1999《汽車制動器 溫度測量和熱電偶安裝》的具體要求,并結合此次研究的重點,分別在制動襯片表面、制動蹄背鋼板面、制動鼓內表面和制動鼓外表面安裝K型熱電偶(測溫范圍:-40~1 300 ℃)。
在靠近制動襯片長寬方向的中心處鉆兩個5 mm的通孔(注意一定要避開筋和散熱片),將熱電偶測量端固定在孔內,偶頭距離制動襯片摩擦表面和制動蹄背鋼板面都為1 mm。在制動鼓摩擦面寬度方向的中心鉆兩個相對于鼓中心對稱的5 mm通孔,將熱電偶測量端固定在孔內,偶頭距離制動鼓內、外表面為0.3~0.5 mm。制動器安轉位置和制動器試驗臺架分別如圖1和圖2所示。

圖1 制動器安轉位置

圖2 制動器試驗臺架
1.3 試驗方法與步驟
由于制動器制動襯片表面與制動鼓內表面的貼合程度對制動力矩產生很大影響,因此,試驗開始前必須保證制動鼓內表面的圓跳動控制在10絲以內,制動襯片與制動鼓內表面的間距約為0.5 mm。同時,在進行模擬長下坡持續(xù)制動的熱衰退試驗開始前,需要先進行磨合試驗,保證制動襯片與制動鼓內表面接觸良好。
長下坡持續(xù)制動的熱衰退試驗主要模擬在長下坡路段汽車持續(xù)較長時間重復制動以達到控制車速的目的。目前,重型商用車的額定工作氣壓已經普遍提高到1.0 MPa,為了能夠更真實地還原持續(xù)頻繁制動過程,試驗氣壓設置為0.7 MPa,制動周期設置為1 min,各種速度下進行15次全制動,同時記錄制動力矩、制動蹄片和制動鼓的溫度。
1.3.1 磨合試驗
(1)制動初速度50 km/h;
(2)試驗冷卻風速11 m/s,冷卻空氣的溫度為室溫;
(3)調整制動管路壓力,使制動減速度達到0.3g,從制動初速度進行制動,到終速度為零;
(4)制動間隔時間以控制制動器初溫不超過100 ℃而定;
(5)磨合次數(shù)以使制動襯片與制動鼓之間的接觸面積達到80%以上而定,磨合試驗次數(shù)一般設置為500次。
1.3.2 模擬長下坡持續(xù)制動的熱衰退試驗
(1)制動初速度40、50、60、70 km/h;
(2)采用恒定輸入方式進行試驗,調整控制氣壓為0.75 MPa,從制動初速度進行制動,到終速度為零;
(3)首次制動溫度不高于60 ℃,在第一次制動進行前關閉試驗臺冷卻系統(tǒng),整個試驗過程中不對制動器吹風降溫;
(4)制動周期設置為1 min;
(5)各種速度下各進行15次全制動。
2 數(shù)據處理與分析
根據戈若愚等通過實車測試發(fā)現(xiàn)影響制動鼓溫度的因素主要包括車輛載重、行駛速度、坡長和坡度。由于臺架試驗的限制無法模擬坡度,因此文中主要從車輛載荷、行駛車速、制動距離這3個方面進行分析。從模擬長下坡持續(xù)制動過程的試驗條件可知,輸入氣壓恒定,因此可分析多次反復制動過程中制動器溫度與上述三者之間的關系。
臺架試驗中分別采集了制動鼓內表面、外表面、襯片表面和背筋板面的溫度,通過對制動器滿載、車速60 km/h情況下4個位置的溫升情況分析,可以看出制動鼓內表面溫度的變化最顯著,鼓外表面溫度次之,制動蹄背鋼板面的溫度變化靈敏度最低。此次研究以制動鼓內表面溫升為主要研究對象。制動器4個不同位置溫度變化情況如圖3所示。
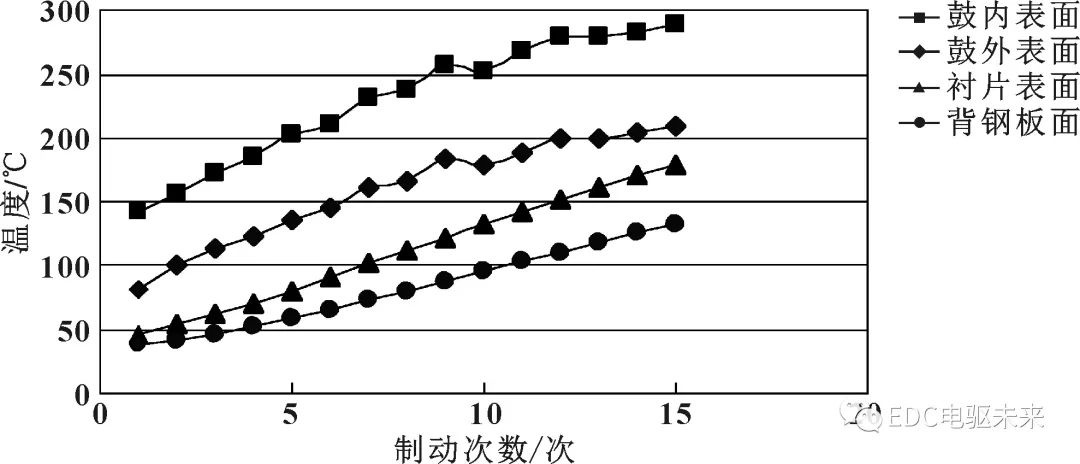
圖3 制動器4個不同位置溫度變化情況(滿載,車速60 km/h)
2.1 車輛載荷
由圖4制動鼓內表面溫度與載荷的關系曲線可以看出:當行駛速度一定時,由于車輛載荷的增加,其存儲的動能更多,車輛制動過程中轉換的熱能越多。所以,在制動距離和行駛速度不變的情況下,制動鼓內表面的溫度隨載荷的增加而上升。
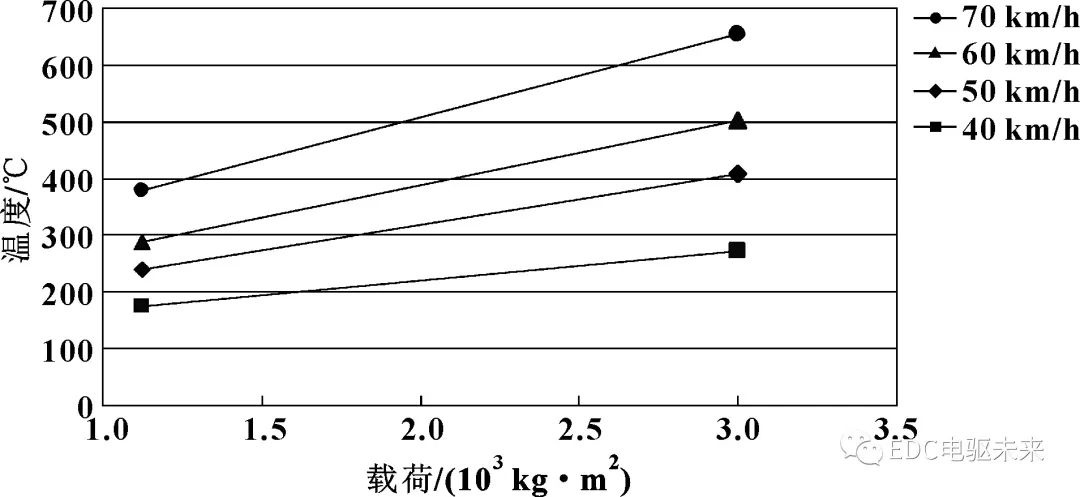
圖4 制動鼓內表面溫度與載荷的關系曲線(制動距離1 500 m)
2.2 行駛車速
由圖5制動鼓內表面溫度與車速的關系曲線可以看出:當載荷一定時,由于車速的增加,初始狀態(tài)具有的動能更大,車輛制動過程中由動能轉換的熱能也更多。所以,在載荷和制動距離一定的前提下,制動鼓內表面的溫度隨速度的升高而增加。
2.3 制動距離
由圖6制動鼓內表面溫度與制動距離的關系曲線可以看出:當載荷和車速一定時,由于制動距離的改變導致制動次數(shù)增加,制動鼓內表面與襯片的摩擦時間變長,其表面溫度隨制動距離的增加而上升。
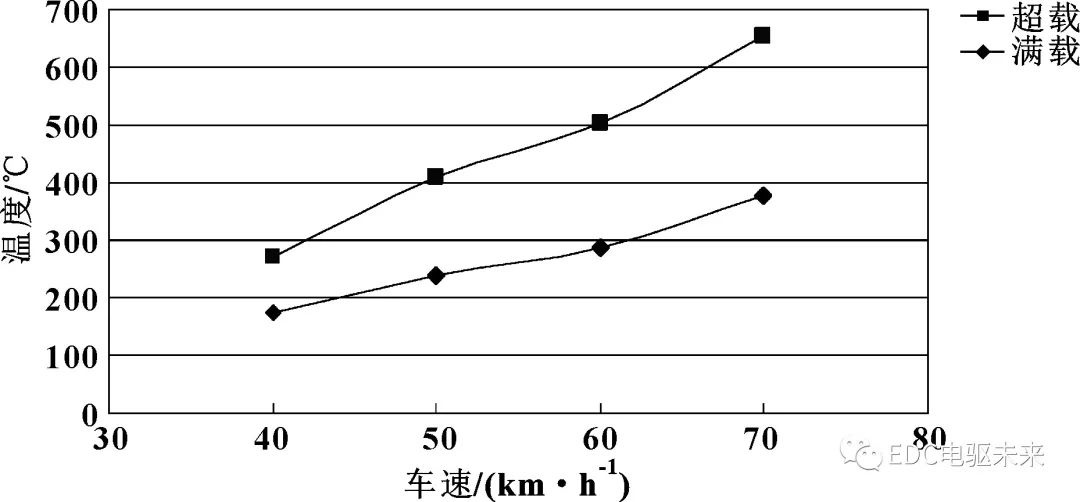
圖5 制動鼓內表面溫度與車速的關系曲線(制動距離1 500 m)
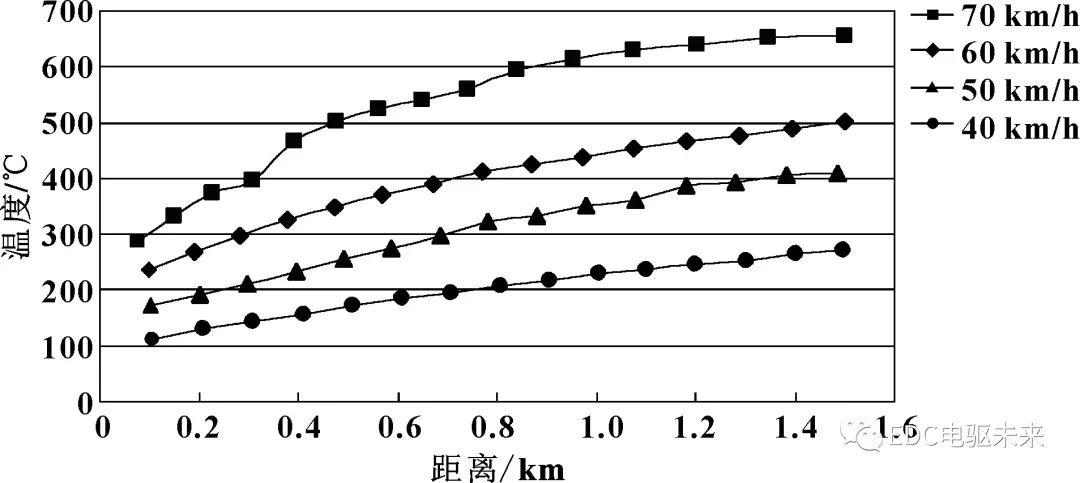
圖6 制動鼓內表面溫度與制動距離的關系曲線(超載)
3 建立制動鼓升溫模型
經過上述的數(shù)據處理和分析,發(fā)現(xiàn)制動鼓內表面溫度與車輛載荷、行駛速度和制動距離都存在一定的關系。利用試驗臺架采集的大量試驗數(shù)據,采用統(tǒng)計數(shù)多元線性回歸方法,在SSPS軟件上采用逐步篩選策略進行分析。設制動鼓內表面溫度T(單位℃)、車輛軸荷G(單位t)、行駛速度v(單位m/s)、制動距離S(單位m),則模擬長下坡制動鼓溫度的數(shù)學模型可以設置為
T=b0+b1G+b2v+b3S
式中:G、v、S為自變量;T為因變量;b0為截距,即常量;b1、b2、b3為回歸系數(shù)。
將制動距離S、行駛速度v以及車輛軸荷G依次引入模型,當每次引入1個變量后都進行F檢驗,并對模型內的變量逐個進行t檢驗,如果當原來引入的變量由于后面變量的引入變得不再顯著時,則將其刪除,這是一個反復的過程,直到既沒有顯著的變量選入回歸方程,也沒有不顯著的變量從回歸方程中剔除為止。輸入和移除的變量如表4所示,其中因變量是溫度。
表4 輸入/移除的變量

回歸方程中復相關系數(shù)R為0.969,決定系數(shù)R2為0.940,調整決定系數(shù)R2為0.938,標準估計的誤差為33.333。R2越接近1,所反映的兩個變量的共變量比例越高,模型和數(shù)據的擬合程度越好。R2=0.940,表示整個回歸方程能夠解釋制動鼓內表面溫度的94.0%。模型匯總如表5所示,其中因變量是溫度。
表5 模型匯總
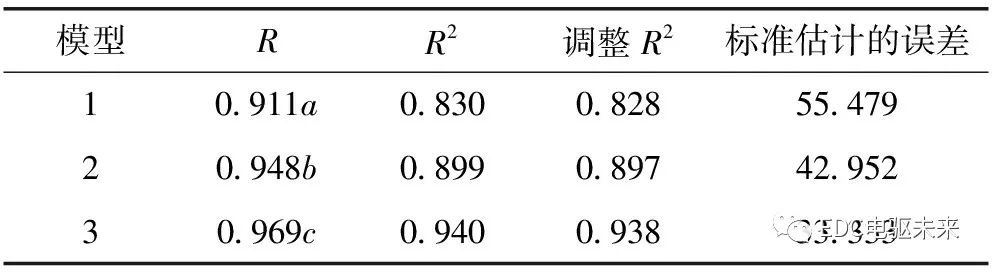
注:a.預測變量:(常量),距離;b.預測變量:(常量),距離, 速度;c.預測變量:(常量),距離, 速度, 載荷。
方差分析表顯示出各模型中對多個自變量的總體檢驗, Sig值為0.000,即完全有把握認為回歸方程是有用的;F值為601.146,查F分布表得F0.05(3,116)=2.68,即F>F0.05(3,116),即可判定回歸方程中的各個自變量聯(lián)合起來對因變量有顯著影響。方差分析表如表6所示,其中因變量是溫度。
表6 方差分析表
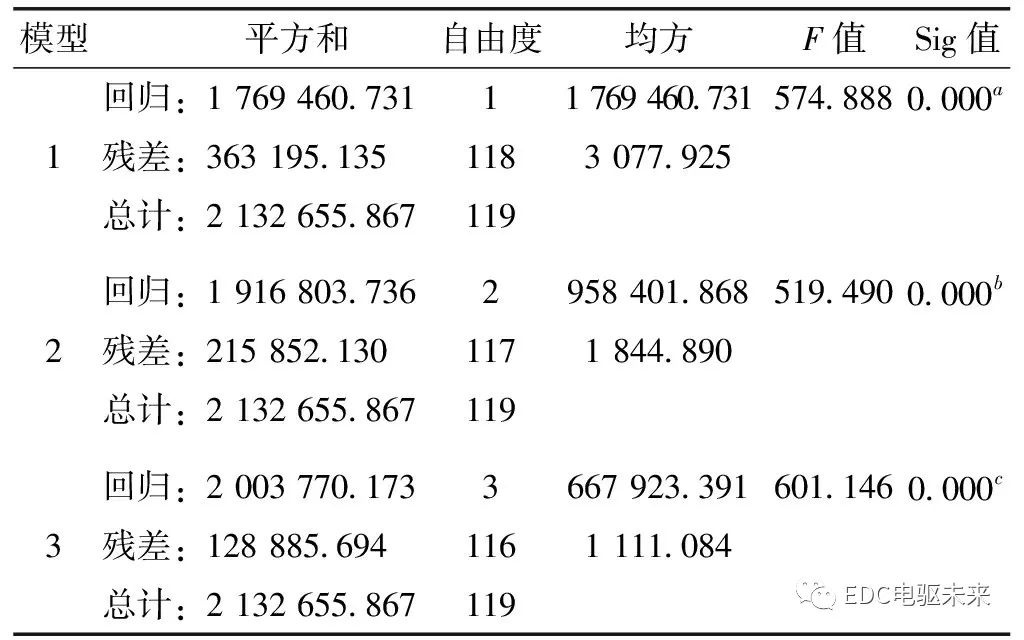
注:a.預測變量:(常量),距離;b.預測變量:(常量),距離, 速度;c.預測變量:(常量),距離, 速度, 載荷。
系數(shù)表羅列出常量、非標準化回歸系數(shù)、標準化回歸系數(shù)、回歸系數(shù)檢驗的t統(tǒng)計量觀測值和響應的概率值。根據模型建立的多元線性回歸方程為
y=-92.547+5.215x1+14.926x2+0.086x3
方程中的常數(shù)項為-92.547,回歸系數(shù)b1為5.215,b2為14.926,b3為0.086,經t檢驗,顯著性概率P值均為0.000,按照顯著性水平為0.05的情況下,即可判定回歸方程中的各個自變量都對因變量有顯著影響。系數(shù)表如表7所示,其中因變量是溫度。
表7 系數(shù)表
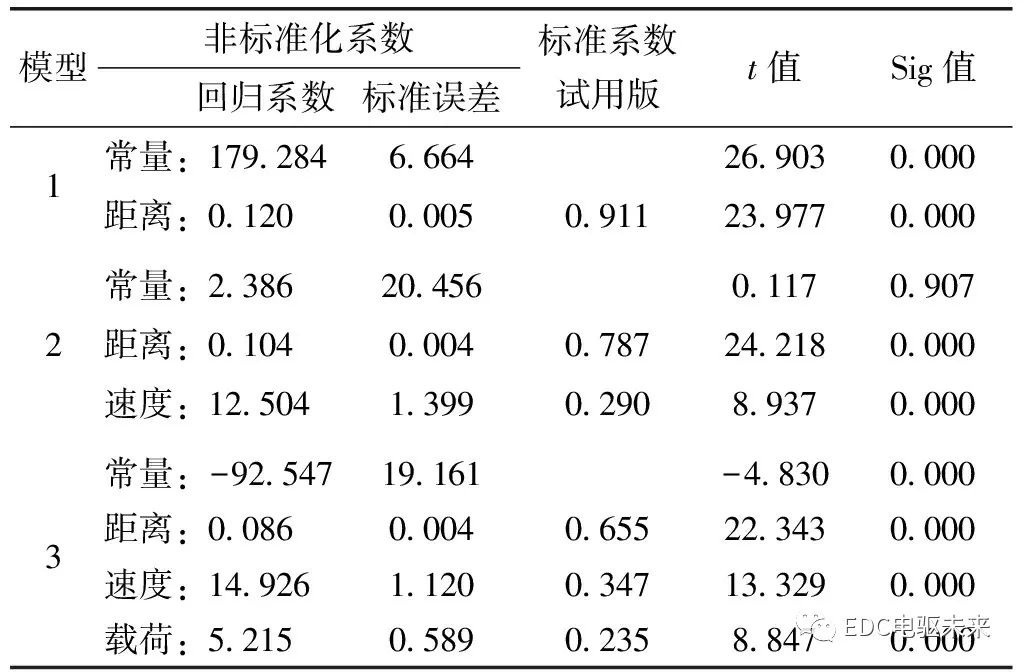
綜上所述,回歸分析得到的回歸方程為
T=-92.547+5.215G+14.926v+0.086S
式中:T為制動鼓內表面溫度,℃;G為車輛軸荷,t;v為行駛車速,m/s;S為制動距離,m。
4 結論
此次研究通過臺架試驗的方式模擬了重型商用車長下坡持續(xù)制動的工作過程,設計了一套完整的試驗方法并采集了大量試驗數(shù)據,分析出制動鼓內表面溫度與載荷、車速和制動距離的關系;運用統(tǒng)計學中多元線性回歸的方法,利用SPSS軟件建立了制動鼓內表面溫度與上述三者的預測模型。預測的溫升模型為實車制動路試以及整車制動系統(tǒng)的匹配提供參考。





