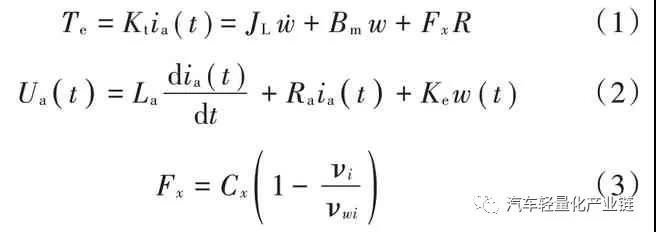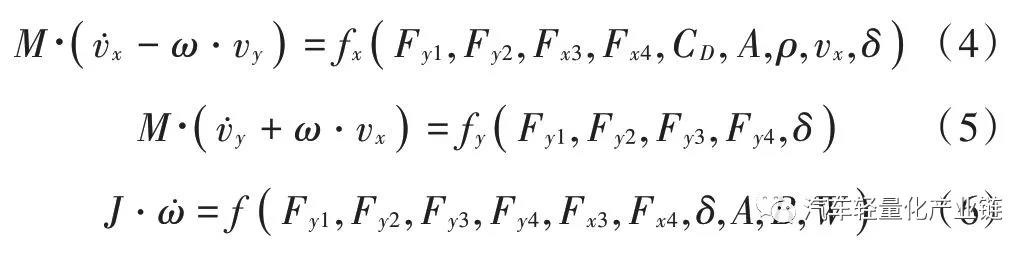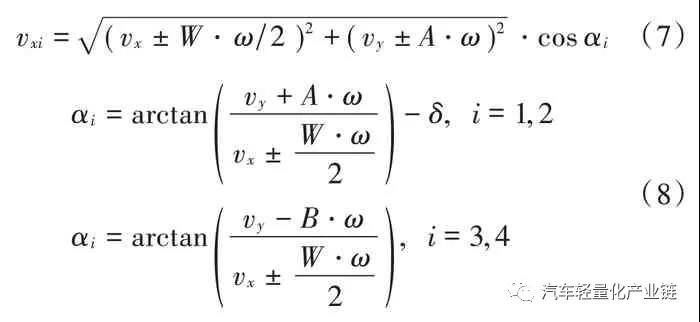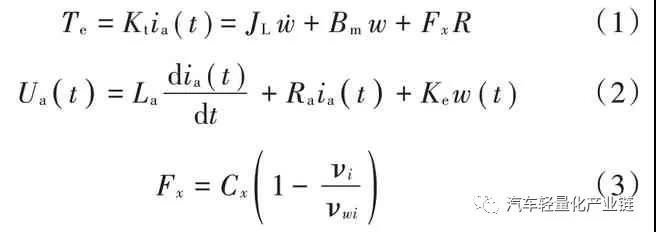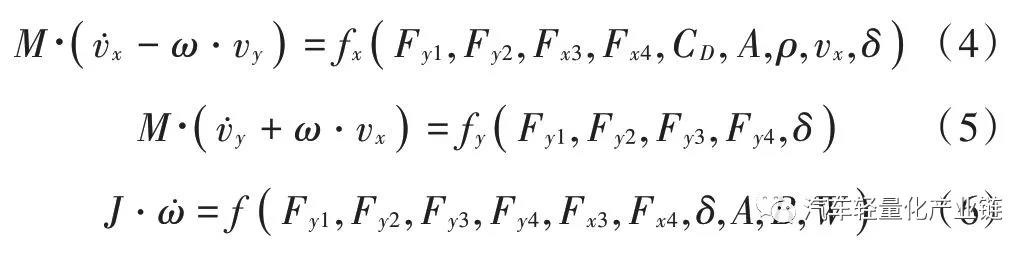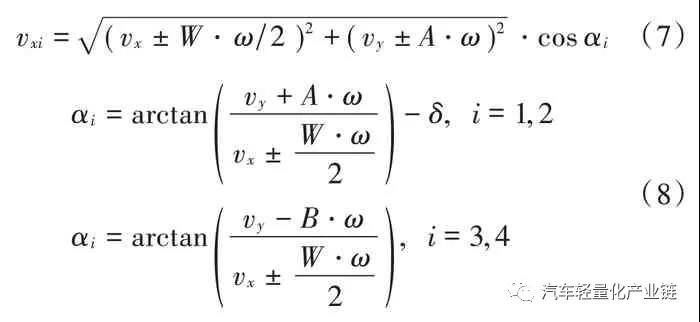信息中心


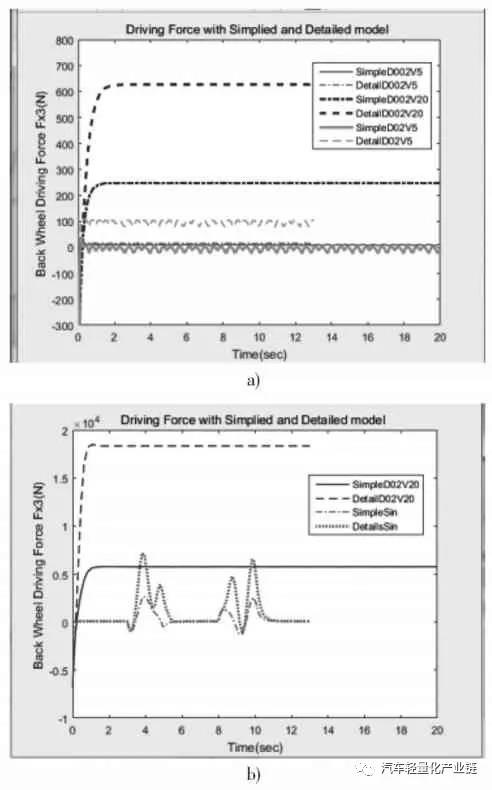
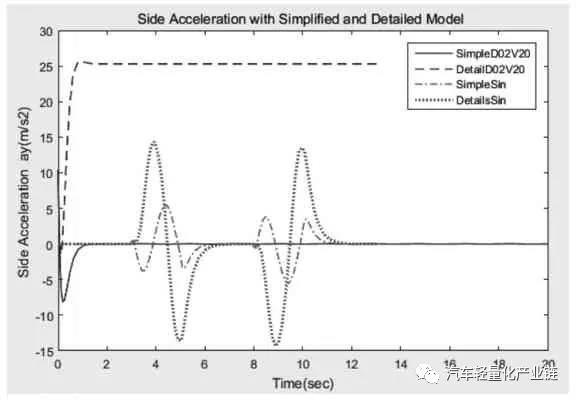
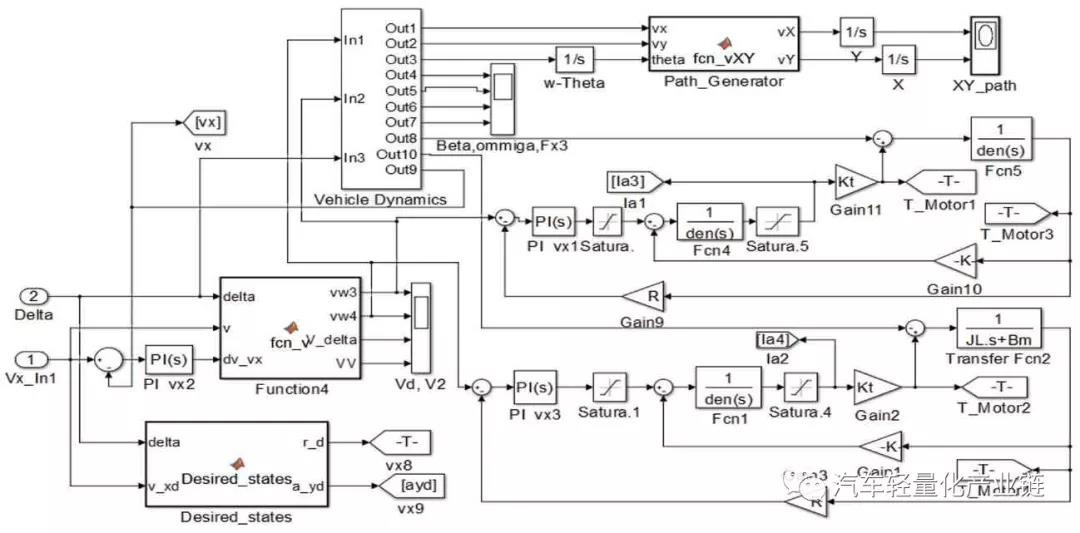
鼓式制動器、摩托車剎車圈、Drum brake、輪轂剎車圈專業生產廠家無錫九環2022年1月25日訊 文中研究分布式后輪輪轂驅動電動汽車轉向控制特性。首先建立驅動電機和車輛動力學模型,分析簡化的動力學模型和非簡化動力學模型在不同轉角和速度時的輸入輸出特性。將整車動力學模型、兩個輪轂電機的機電特性模型集成起來,形成兩層三環節的控制。外層進行行駛速度反饋控制,內層進行兩個電機轉速的反饋控制,外層的總行駛速度經過速度分配,作為內層兩個電機轉速的輸入分別控制兩個驅動電機,車輪的轉矩作為電機的負載轉矩輸入。最后對三種模型在兩種轉角變化工況下的動力學響應進行對比分析。關鍵詞:輪轂電機;電動汽車;PID 控制;直流電機;電子差速;轉向控制輪轂電機是將電動機和制動系統集成在車輪上進行直接驅動的裝置,20 世紀60年代后期應用于大型的礦用自卸車上。近幾年,隨著電動汽車的迅速發展,輪轂電機由于其控制靈活獨立、可以分別控制和協調各輪的運動,開始用于電動汽車形成分布式驅動的電動汽車。這種驅動形式的電動汽車在結構上去掉了汽車底盤中的機械差速和隨動系統等傳動裝置,大大簡化了汽車的結構,降低了汽車的重量,是對傳統的集中驅動汽車結構的較大革新,具有極大的應用潛力,成為新型電動汽車的研究熱點。目前的研究主要有輪邊電機驅動與輪轂電機驅動兩種形式[1-2],輪轂電機驅動是將驅動電機直接安裝在車輪中,不占用車身空間,對電機和輪轂的設計和電機的控制要求都較高。為提高汽車的操縱性能和穩定性,需要針對當前的行駛狀態和駕駛員的駕駛指令,精確快速地控制每個輪的速度和扭矩,因此電機機電特性、硬件的響應速度、轉向、加速、啟動、剎車時的速度或者扭矩的分配[3-4],都是要實時監測或者協調控制的多個變量。目前成熟的技術主要用于低速緩慢的大型重載工程汽車和裝甲車上,研發的熱點和難點是將分布式輪轂驅動用于城市交通電動汽車上。文獻[5]將BP神經網絡用于轉速分配及控制,可用于和學習樣本類似的車輛情況和路況。文獻[6]根據橫擺角速度、橫向加速度與參照速度的誤差值和后續的PI 控制環節進行轉矩分配。文獻[7]根據橫擺角速度、質心側偏角與參考值間的差值,采用滑模控制來計算所需要的總橫擺力矩,優化分配各個輪胎受力。目前的研究基本是在特定的車輛實例中針對某一個目標,例如滑移率[8]、側向力[8]、橫擺角速度等,進行轉矩分配或者轉速分配來提高車輛操縱性和穩定性,控制效果滿意。但控制模型及控制參數的調整,動力學特性和動力學參數,包括電機的參數和選擇千差萬別,沒有通用的參照可以使用,而且很多研究只考慮車輛的動力學,忽略電機本身的動力學特性和車輛動力學特性的耦合,把驅動電機看作是一個理想的完美驅動單元[9]。本文在前期輪轂電機驅動研究的基礎上[10-12],首先分析整車動力學模型,在整車動力學模型上增加了直流電機驅動模型,把驅動電機機電特性和車輛動力學模型集成起來,針對后輪輪轂電機驅動的特定車輛,在特定行駛速度下仿真分析轉向情況下的穩定性控制特性。電動汽車的可靠行駛和操控要求輪轂電機具有寬的調速范圍、足夠大的啟動轉矩、體積小、重量輕,制動性能好,且具有能量回饋的特性。本文主要研究直流電機作為后輪驅動,直流電機產生的電磁轉矩帶動車輪旋轉,同時克服由于摩擦產生的阻力和負載轉矩。對電機而言,車輪和地面的摩擦力形成的轉矩為負載轉矩,對車輛來說,這個與輪胎變形相關的摩擦力就是車輪前進的驅動力,機電耦合的電磁轉矩方程、直流電機的電樞回路電壓平衡方程(電方程)如式(1)~式(3)所示:式中:Te 為電磁轉矩,與電樞電流ia(t)成正比;J 為車輪與電機的轉動慣量;R 為車輪半徑;Ua( )t 為電樞電壓;w(t)為電機轉速;La,Ra 分別為電樞電路的電感和電阻;Fx 為車輪縱向摩擦力,當車輪橫向力一定時,縱向力取決于車輪的滑轉率,在滑轉率很小時(對于干路面滑轉率小于 0.1),縱向力與滑轉率成正比[2];Bm,Ke,Kt 分別為粘性摩擦系數、電勢系數和轉矩系數,由電機設計參數得出;i=1,2,3,4,表示汽車的4 個輪子,分別為左前輪、右前輪、左后輪和右后輪;νwi 為車輪轉速;νi 為車輪中心速度平行于車輪平面的分量;Cx 為車輪的縱向剛度。本文研究的是后輪輪轂電機驅動的電動汽車,2 個后輪輪轂上分別安裝2 個直流驅動電機,在驅動轉矩作用下,2 個后輪輪胎受到地面的縱向摩擦力。轉向時,根據轉角及當前的速度,在后輪上分配不同的速度和力矩,形成側向摩擦力,側向摩擦力和縱向摩擦力的合成轉矩完成汽車的轉彎。設x 軸為汽車的前進方向(縱向),y 為與車身垂直的水平(橫向)方向,汽車行駛或者轉彎時,車輛中心具有縱向平動(縱向速度為Vx)、橫向平動(橫向速度為Vy)和在地平面中繞z 軸的轉動(橫擺角速度為ω)三個自由度方向的運動,考慮車身受到的空氣阻力,可得到以下縱向運動、橫向運動和橫擺轉動的動力學方程組[13]:式中:δ 為前輪轉向角;A 為車輛質心到前軸的距離;B 為車輛質心到后軸的距離;W 為左右輪距;M 為車輛質量;J 為車輛轉動慣量。在縱向運動方向上考慮空氣的阻力,與空氣阻力相關的參數分別為空氣阻力系數CD,車輛正面迎風面積A,空氣密度ρ。每個車輪的中心沿著車輪縱向的速度由式(7)計算,由于車輪的側向彈性形變,車輪中心速度與車輪平面成一夾角,形成車輪的側偏角αi,具體計算如下:當車輪側偏角較小時輪胎側偏特性處于線性區,車輪受到的垂直方向的力一定時,側向力Fyi 與側偏角成正比[14],比例系數Cy 為車輪的側偏剛度,本文取輪胎摩擦公式的線性段的斜率值。一般文獻進行計算分析時,為了降低計算難度,通常忽略橫向加速度和縱向加速度的耦合作用。從公式本身來看,如果轉角和線速度都比較小時,簡化模型可以近似反映運動情況,引起的誤差比較小,但是當轉角或者速度較大時,簡化模型就會產生較大的誤差。如果忽略這種耦合,對直線行駛沒有什么影響,但在有轉彎的狀況下,轉角越大速度越大,誤差越大。分別對轉角為0.2 rad 和0.02 rad,車輛質心線速度為5 m/s 和20 m/s形成的四種行駛狀況,以及雙移線行駛狀況共五種狀態定量分析簡化模型和非簡化模型的動力學特性,求解結果前三種工況組合下左后輪的縱向驅動力Fx3,如圖1所示。由圖1 可以看出,當轉角很小δ=0.02 rad,行駛速度很小v=5 m/s 時,兩種模型的縱向驅動力差別很小,簡化模型作為力學模型引起的誤差很小,可以忽略。當速度增加到20 m/s 時,簡化模型的縱向驅動力為200 N 以上(SimpleD002V20),而非簡化模型的縱向力需要600 N以上(DetailD002V20),增加了2 倍,轉向和縱向運動的耦合不容忽視。繼續觀察δ=0.2 rad 時,v=5 m/s 和v=20 m /s 時 的 曲 線(SimpleD02V20 和 DetailD02V20,SimpleD02V5 和 DetailD02V5),可以看出隨著轉角 δ 和速度v 的增加,簡化模型和詳細模型中縱向驅動力的差別也會增大;圖1b)的雙移線運動狀況是速度不變、轉角進行兩個周期的正弦變化時的縱向驅動力結果,可以看出,縱向驅動力的差別也是隨著轉角的增大而增大。模型的橫向驅動力和側偏角也是隨著轉角和速度的增大而增大。圖2 為側向加速度的比較,可以看出,行駛速度較大時,兩種模型的橫向加速度是有一定的相位差的,即在正弦變化的轉角輸入中,兩種模型達到最大橫向加速度的時間不同。由此可見,在轉角較大、速度較大時,簡化模型已經不能準確及時地反映行駛的動力學特性,因此本研究在后續的控制模型中采用反映橫向運動和橫擺角速度耦合的詳細模型。整體動力學及控制模型如圖3 所示,圖中整車動力學模型封裝為子模型。在詳細動力學模型中,給總體行駛速度加上速度反饋及PI 控制,形成第一層外環的速度控制,再把兩個驅動電機及其控制模型集成到整個模型的車輪部分中,把后輪3 和后輪4 的車輪速度和車輪負載分別作為兩個驅動電機模型的輸入,根據設定的速度和轉角,采用Ackermann 模型進行兩個后輪的速度分配,形成兩個驅動電機的速度參考,每個電機的輪速反饋和PI 控制形成第二層內環的兩個控制環節,形成后輪輪轂驅動的整體電動汽車控制模型。車輛的主要參數及根據車輛要求設計的直流電機主要參數為:M=1 500;A=1.6;B=1.4;W=1.6;J=3 375;R=0.3;Ke=4.5;Kt=43;La=0.012;Ra=1.2;Bm=0.005,控制參數根據模型進行整定和優化。仿真分析中對三種控制模型進行對比:第一種是沒有速度反饋的原始模型;第二種是只加一層速度反饋而沒有集成兩個驅動電機模型,把驅動電機作為一個理想的驅動單元;第三種則是本文具有兩層反饋三個控制環節的模型(見圖3)。在后續的仿真分析對比中,第二種只有一層PID 控制的數據標記為with PID,第三種集成車輛模型和電機模型的數據標記為with PID and Motor,剩下的數據為沒有速度反饋環節的第一種原始模型。仿真分析中的汽車穩定性系數Kus 由回歸得出,側向剛度和縱向剛度取輪胎魔術公式中的斜率部分,路況為干性平坦路面。本文主要分析轉彎時的控制,工況為行駛速度恒定下的兩次變道雙移線,速度設為v=20 m/s=72 km/h。轉角變化分析兩種情況:第一種是轉角突然階躍變化左-右-直-右-左,實現兩次變道;第二種是把階躍變換調整為相同頻率的正弦變化,峰值為7°,頻率為0.5,兩個正弦波之間隔1.5 個周期,即直行1.5 個周期,兩種輸入狀態下的轉角如圖4 所示。圖5 和圖6 分別顯示兩種輸入模式下三種模型的后輪驅動力和橫向加速度曲線對比。可以看出,對于表示突然轉向的階躍輸入,會引起加速度響應的突然變化,驅動力變化曲線不平穩,有突然變化的尖角,導致側向不穩定;調整成為正弦變化雙移線后消除了曲線尖角,驅動力曲線平緩很多,幅值也有較大程度的下降,車輛的穩定程度有明顯的提高,這和一般的駕駛體驗相符,說明控制模型能正確模擬實際的狀況。第三種模型和第一種模型的側向加速度幅值比第二種模型小點,但是第一種模型因為沒有反饋環節,因而無法跟蹤參照速度,導致縱向速度略微降低,穩態誤差加大,即犧牲一部分縱向速度,達到減少側向加速度的目的。綜合比較,第三種模型縱向速度始終跟隨參照速度,同時側向加速度也比其他模型小,因此轉向穩定性較好。
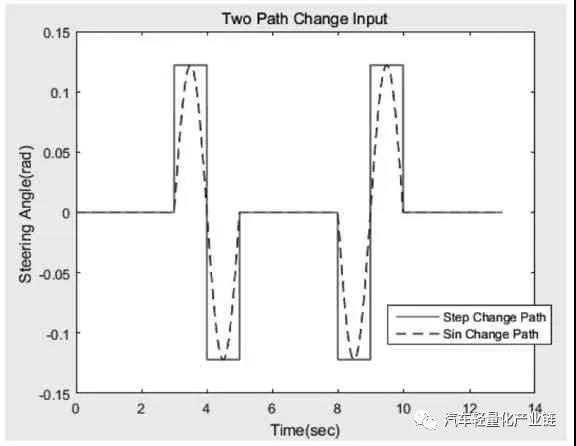
圖4 轉角輸入階躍變化和調整后的正弦變化
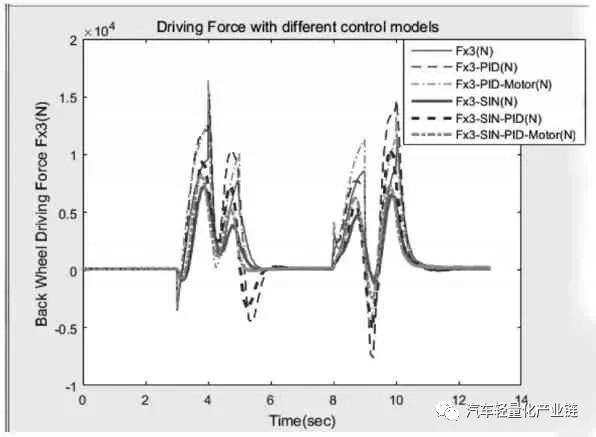
圖5 轉角階躍和正弦響應的后輪驅動力
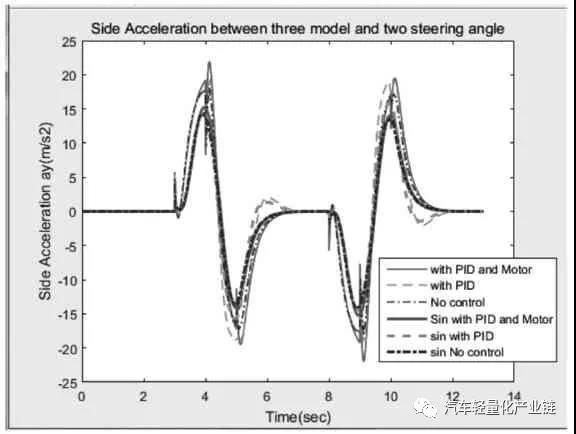
圖6 轉角階躍和正弦響應的側向加速度
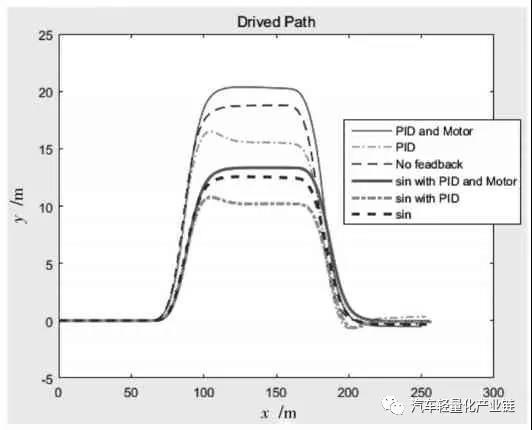
圖7 顯示了三種模型兩種輸入的雙移線軌跡。首先比較正弦調整的轉角輸入和階躍變化工況,由于正弦轉角變化相對減緩且數值偏小,導致橫向加速度變小進而橫向速度變小,因而y 方向的位移相應減少;對于有PID 和電機模型的兩層三控制環節模型,由于行駛速度和單個輪速的及時反饋和補償,縱向速度和橫向速度都能跟蹤參照速度,不足轉向和過度轉向能夠得到及時控制,因而y 方向的位移是三個模型中最大的,也就是說,達到相同的y 方向位移的參照速度可以降低;對于只有外層控制環節的第二種模型,由于不能及時調整兩個輪子的速度,同樣輸入情況下會出現過度轉向或轉向不足的情況。本文建立并集成了驅動電機模型和整車動力學模型,形成后輪驅動整車控制模型。考慮通常的忽略橫向加速度和縱向加速度的耦合作用,量化分析簡化模型和非簡化模型在不同轉角和速度時的輸入輸出特性,認為在轉角和速度較大時,簡化模型不能準確及時地進行動力學控制,因此本文采用反映橫向運動和縱向運動耦合的詳細模型。在控制框架中,輪速和與輪速相關的負載轉矩作為機電模型的輸入,外層進行總行駛速度反饋控制,內層進行兩個電機轉速的反饋控制,形成一個兩層三環節的控制模型,外層的總行駛速度經過內外輪的速度分配即電子差速,作為內層兩個電機轉速的輸入分別控制兩個驅動電機。最后對三種模型在兩種轉角變化工況下的動力學響應進行對比分析,驗證了該控制方法可以達到預期的效果。
[1]李以農,楊陽.電動汽車底盤一體化控制技術的發展趨勢與展望[J].世界科技研究與發展,2016,38(3):481-491.[2]楊世春.電動汽車設計基礎[M].北京:國防工業出版社,2013:24-25.[3]徐寅,陳東.電動汽車差速系統研究綜述[J].中國機械工程,2011,22(4):498-503.[4]袁儀,陳世元,劉耀閣.電動汽車電子轉彎差速的解決方案綜述[J].上海汽車,2009(3):2-5.[5]唐文武,陳世元,郭建龍.基于BP神經網絡的電動車電子差速器設計[J].汽車工程,2007,29(5):437-440.[6]OSBORNA R,SHIMB T.Independent control of all-wheeldrive torque distribution [J].Vehicle system dynamics,2006,44(7):529-546.[7]余卓平,姜煒,張立軍.四輪輪轂電機驅動電動汽車扭矩分配控制[J].同濟大學學報,2008,36(8):1115-1119.[8]葛英輝,倪光正.新的輪式驅動電動車電子差速控制算法的研究[J].汽車工程,2005,27(3):340-343.[9]KAROGAL I,AYALEW B.Independent torque distribution strategies for vehicle stability control [R].Detroit:Sae World Congress & Exhibition,2009.[10]史秀梅,鄭壽森,祁新梅,等.三相開關磁阻電動機電磁場有限元分析[J].微特電機,2009(12):35-37.[11]熊俊峰,鄭壽森,祁新梅,等.電動汽車開關磁阻電機驅動電源的設計與研究[J].電力電子技術,2009(7):42-44.[12]史秀梅,鄭壽森,祁新梅,等.電動汽車用開關磁阻電機有限元分析及仿真[J].系統仿真學報,2011,23(7):1374-1377.[13]王強,王耘,宋小文.基于差動驅動的電子差速控制方法研究[J].機電工程,2011,28(6):698-703.[14]韋競秋.汽車工程應用力學[M].北京:機械工業出版社,2013:17-18.[15]余卓平,趙治國,陳慧.主動前輪轉向對車輛操縱穩定性能的影響[J].中國機械工程,2005,16(7):652-657.
?